In several areas of science and technology, measuring all relevant quantities in a given system is often not viable, or even possible, due to technological limitations or the sheer amount of data. This in turn leads to the question: is it possible to infer or estimate the unmeasured values using the measured data? According to statistics, mathematics, and control system theory, the answer is yes, and a plethora of different techniques have already been developed, each with its own benefits and drawbacks.
As one of the said estimation frameworks, the modulating function method can be seen as a generalization of the Laplace and Fourier transforms, indicating that it is a powerful mathematical tool for data analysis in general. In simpler terms, this method can be seen as studying objects and their movements through ”mathematical shadows”.
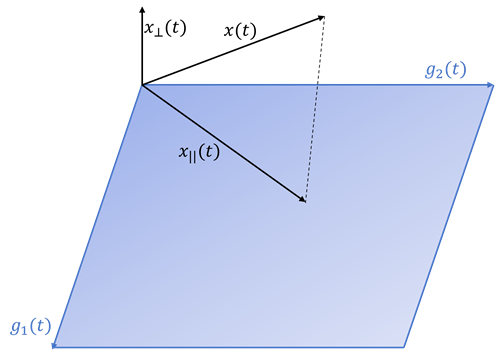
More technically, this method consists of studying some variable x(t) through the ”shadow”, x(t)∥, it casts onto the ”plane” g(t) which, in the case of the example above, is described by two ”directions”: g1(t) and g2(t). In doing so, it is possible to remove the necessity of, for example, derivating noisy measurements, consequently improving estimation reliability by reducing noise amplification. Another intriguing characteristic of the modulating function method is that it is able to obtain the correct estimate in a finite amount of time with ease, a trait that is not often found in traditional estimators for the control system community, known as observers.
So far, this technique has been used to study the system characteristics, formally known as parameter estimation, as well as the system dynamics, i.e. state estimation, of a myriad of physical systems, such as, e.g., reaction-diffusion, air-handling units, and even some classes of nonlinear systems. However, despite all said benefits and applications, the modulating function method has not been explored to the same depths as, e.g., Bayesian estimators or observers, possibly concealing its potential and applications. For that reason, the objective of this project is to further study and develop the modulating function method, investigating its properties and capabilities of application.
This project is supervised by Professor Jerome Jouffroy.
Contact information: Ph.D. student Davi Accioli - email: davi@sdu.dk.